sketchbot
Intermediate Turtle Graphics
Abstraction
One of the most important things in programming within any language is the ability to abstract. The ability to create new compound constructs that are indistinguishable from primitives gives one approach. In this way you can essentially extend the language; defining increasingly intricate things.
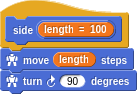
In our Turtle Graphics language here, we have primitives such as move, turn, repeat, … Let’s make a square definition from what we created earlier.
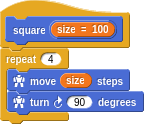
We’ve even parameterized our new word with a size. This way we can reach in and poke values into the defintion without cracking it open. More importantly, without having to know how it works inside. This is how you manage complexity as you make more and more intricate things. We can now use our square within a familiar pattern.
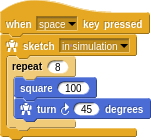
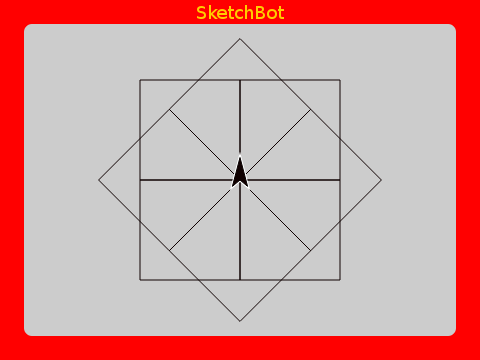
Refactoring
The way it normally goes is that you start out playing around. Maybe to make a rectangle you think of this:
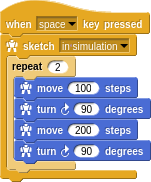
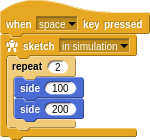
Then you notice that each side is the same two steps but with different parameters. Once you become sensitive to it, the don’t repeat yourself (DRY) principle will make you feel uneasy about even something small like this. So you factor into a new word.
And then reduce the sketch to:
Hey, you may as well name this rectangle sketch and parameterize it by the width and height.
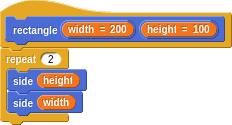
And, oh wait, we can now redefine square to be simply a rectangle with equal sides!

The pretty pattern we made with squares still works with this new definition of square. This is an important point. Any sketch using the definition shouldn’t know or care how it works. You should be free to change the internals without breaking things.
This idea of making rough sketches (so to speak) and then continually refactoring as you add abstractions and discover more succinct ways of describing what you want is one of the great joys of programming.
Generality
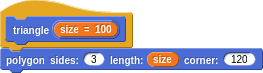
Let’s play with some other shapes. We should be able to make a triangle the same way we made a square, but with fewer sides and tighter turns.
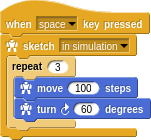
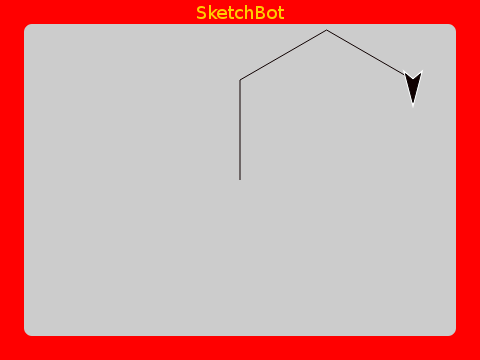
Oops! I was thinking that the interior angles of an isosceles triangle is 60 degrees. Actually the turn angles in turtle geometry are the exterior angles. We just got lucky with the square, where both are 90 degrees. Trying again:
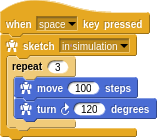
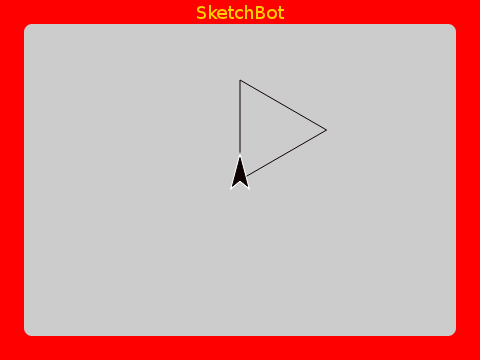
And of course, we should bundle this up and give it a name.
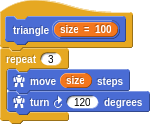
Does anything bother you yet about the definitions we’ve made so far? How is triangle different from rectangle or square? Why can’t we use our side definition here?
At the time, we were thinking only about shapes with right-angled corners and so we assumed side had 90 degree corners. It’s more succinct to make our base definitions as general as possible and then, perhaps, define more specific and specialized things in terms of them.
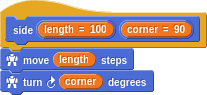
We can then either go into the rectangle definition and hardcode 90, or we could define a new right angle side and define rectangle in terms of this. We’ll leave that up to you.
At any rate, we can now make triangle more succinct:
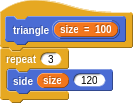
More Generalization
Defining square in terms of rectangle couldn’t really get more concise, but if we go back and rethink things a bit, we might notice that we could have defined it very similarly to triangle:
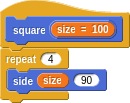

Rethinking what you’ve done and sealed away from time to time is a healty habit. Do you see any generalization we can make here?
Both are really just polygons!

The difference is in the number of sides and the corner angles. A square is a regular quadrilateral.

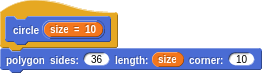
Why not go ahead and define a pentagon, hexagon, etc. Even a circle can be approximated as we did earlier as a many sided polygon.


“Smart” Words
There is still something about these definitions that should bother you! Why is it that polygon must know the number of sides and the corner angle to use? Isn’t the angle always 1/side of the (360) way around?

You don’t want to be too smart, however! Notice that we define regular polygon in terms of the more explicit polygon. While it’s nice to not have to specify the corner angles, we don’t want to lose the ability to make things such as five-sided polygons that are not pentagons:
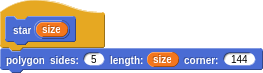
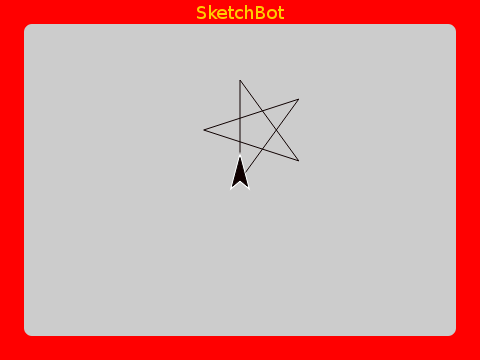
This is yet another general principle. It is well and good to hide details to make things “simpler”, but you don’t want to lose capabilities in the process. Build layers atop layers, but without forbidding access to useful layers below.
Now the various concrete polygons can be defined in terms of general regular polygon and have less internals of how things work embedded in them.




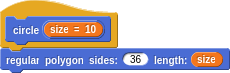
Fun!
You can see that this constant refactoring can be quite fun! It’s almost always the case that you start out with a few concrete instances of something and then realize the general idea. Humans are excellent at generalizing from examples. Don’t feel bad at all about having build things only to tear them appart and rebuild atop new generalizations. This is all part of the fun!