sketchbot
Recursion
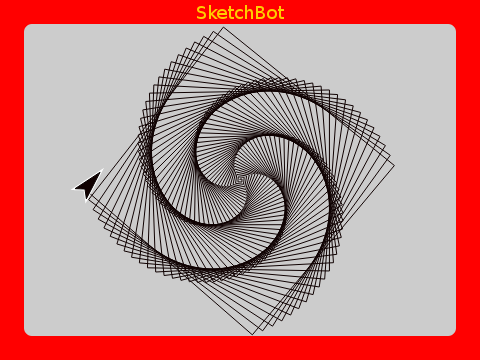
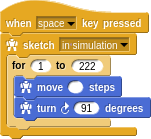
Take a look at this tiny sketch. It’s rather amazing that just a few commands can result in such striking art.
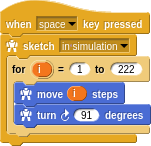
The for loop runs the program within 222 times with i representing the iteration number. This is a common construct in many programming languages.
This is not the only way to express iteration however. Some software developers are uneasy about the fact that i keeps changing in place. In mathematics this is like saying x = x + 1 which makes no sense! There is no x for which this “equation” is true.
The Functional Way
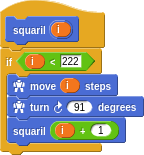

This functional definition relies on recursion. In fact, recursion is the only way to achieve loops in a pure functional sense. Notice that the definition of squaril refers to itself at the end! To read this, you think to yourself that squirl of i (as long as i < 222) means to move i steps and turn 91 degrees followed by another squaril of i + 1.
Another, more inductive way to think of it is to say, “Assuming you know how to make a squaril of i + 1, then you know how to make a squaril of i. It’s just blah, blah followed by what you already know, and this is true for any i < 222.” This kind of “deferred” thinking where you assume you know how to handle the recursive case and then can inductively handle the current case is often a useful way to think about it.
In any case, unless you want infinite recursion, you always have a base case that ends the process. In this case it’s when i >= 222.
Side note: If you’ve been taught that recursion is bad because you can “blow the stack” then you should take the time to learn about tail call elimination and fear not!
How Do For Loops Work?
Do you remember when we said that being able to define new words that are indistinguishable from primitives is one of the primary means of abstraction? You probably think that the for loop is a primitive. Try right-clicking (or CTRL-click) and Edit... it.
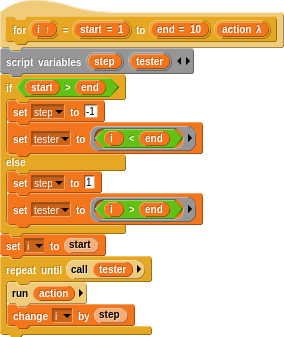
There’s a bit of a mess in there to handle reverse loops where the start is greater than then end. If we strip that out, it’s essentially:

The change i by 1 is the “impure” part. It’s the x = x + 1. Here’s how to do it functionally:
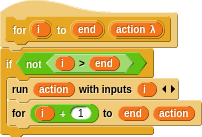
This is a higher order word, as we learned about earlier, taking the i and end values and an action body. The base case is when i reaches end. The action is passed the current iteration (i) explicitly and this is incremented on each recursion. That’s it!
How exactly do you pass an action taking a parameter? There’s a trick of sorts in the language in that simply leaving a slot empty yields a function taking a parameter.
Have fun sketching!