sketchbot

Fun with Fractals

Once we’ve learned about recursion, fractals are a beautiful way to play. A fractal is just a pattern that is “self similar” when we look at it from different “zoom levels”.

Koch Curve

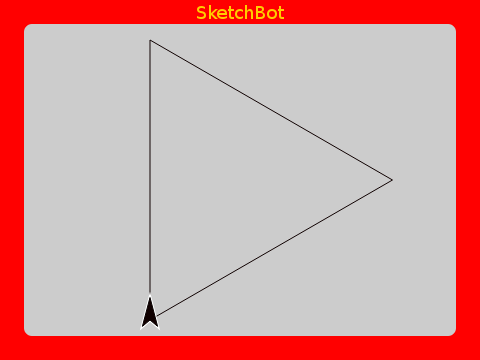
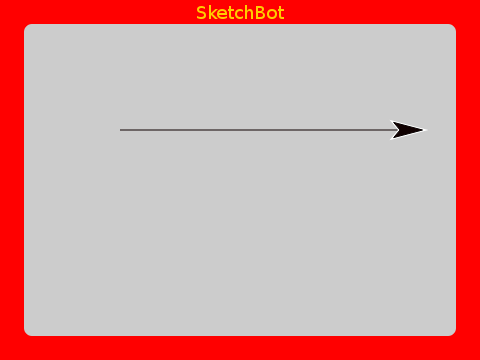
Starting with a straight line:

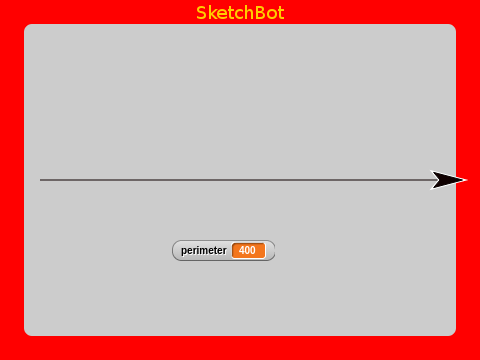
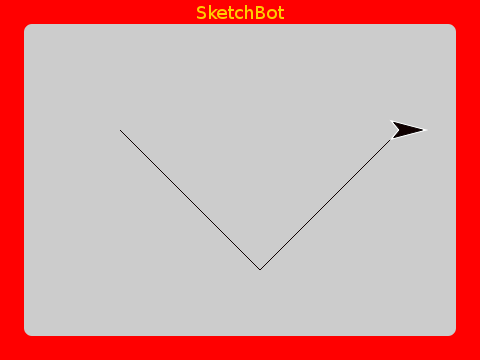
If we divide it into thirds and make a triangle bend in it like this:

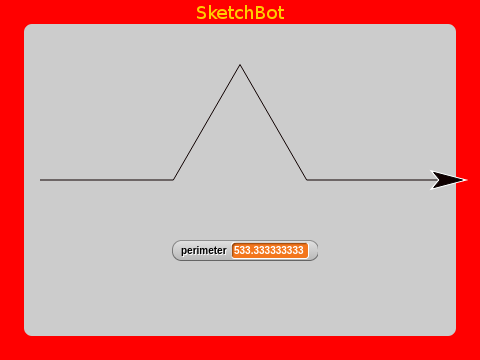
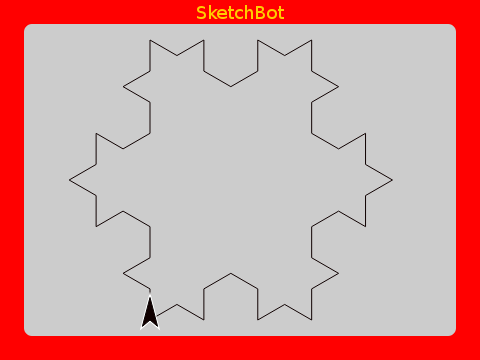
We’ve increased it’s length by a third (look at the perimiter value). If we take each of the line segments now and do the same, we start to make an interesting pattern:

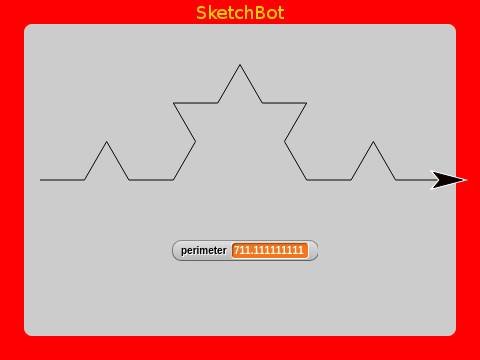
Again, we’ve increased the length by a third (because we’ve increased each segment by this).

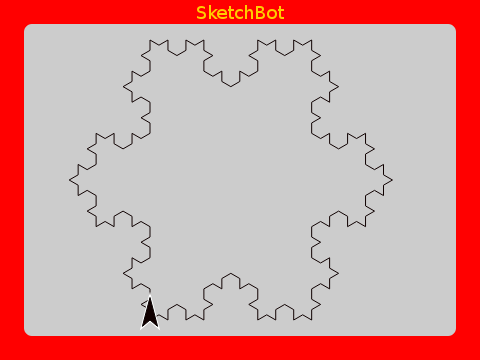
This is a fractal called a Koch Curve. Notice that it is self-similar to the previous instance; by being made of four of them. Continue doing this an we get an increasingly intricate pattern; each a third longer than the last.

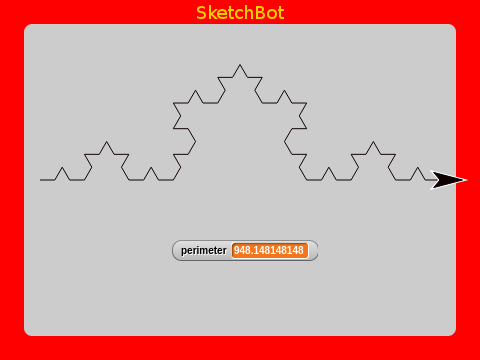
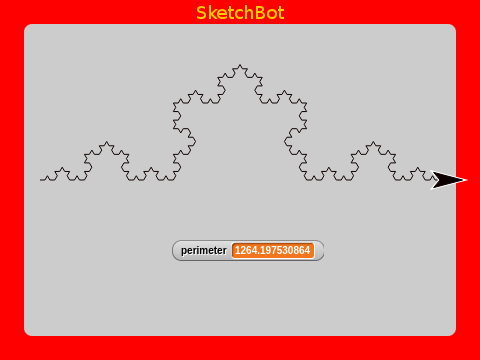
The very interesting thing to notice is that as we continue, the length continues to grow by 4/3, but it continues to fit on the Etch A Sketch screen. You can imagine repeating this an infinite number of times and we would theoretically get an infinitely long curve!

It can’t be seen on the screen, but here is ten iterations. See that the perimiter has grown to more than 7101!

How do we draw such a complicated beast? Well, the self-similarity is begging for recursion to be used.

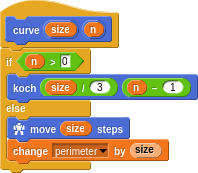
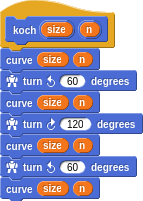
In this case, we’re using mutual recursion. The curve is defined in terms of koch, which is itself defined in terms of curve again. Notice though, that n is decreased with each iteration and that when it’s ≤ 0 then the curve is a simple line like we started with.

The perimeter variable is set to 0 initially and tracks the distance traversed; the sum of all the line segments of length size.

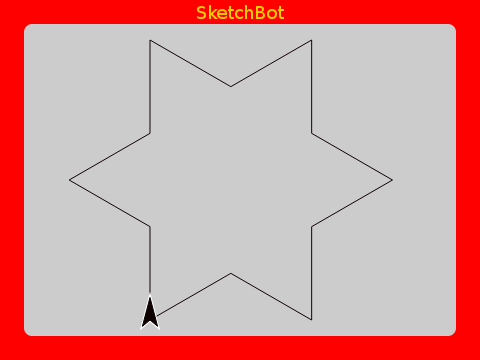
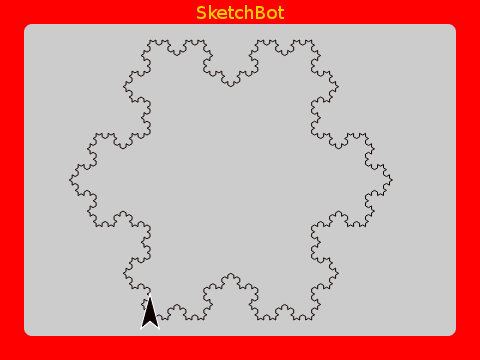
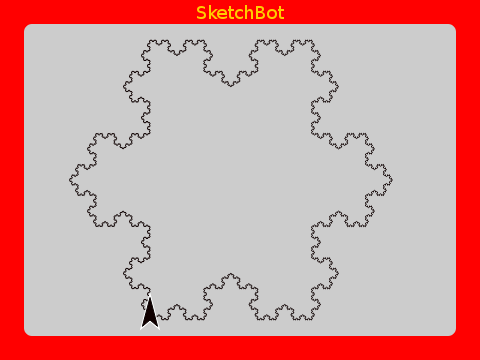
Koch Snowflake

A well known fractal using the Koch Curve is the Koch Snowflake. It’s just an equalateral triangle with Koch Curves for sides. Very cool!

This is interesting for the same reason as the Curve. As the number of iterations increases (possibly to infinity), the perimeter increases, but the area of this closed shape remains finite. A shape with a finite area, but an infinite perimeter. Very strange indeed!

This is a very important concept in mathematics. Knowing that the area grows by less and less with each iteration tells us that it converges at some finite value, while the perimeter grows at a constant rate and so never converges. This concept of knowing the limits of a process is an important one in calculus and a small bit of intuition gained from this example might prove useful later!

Hilbert Curve

The Hilbert Curve too is a fractal with self-similarity. It is what is known as a space filling curve. Here’s how it goes.

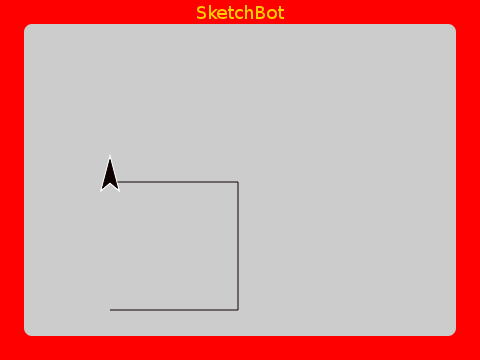
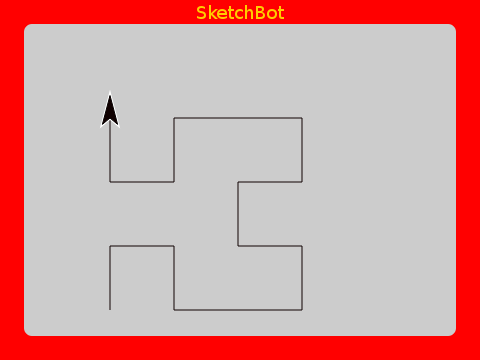
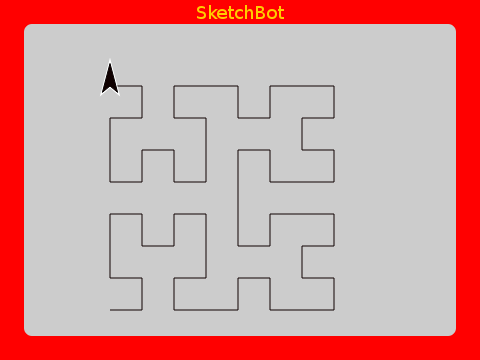
As the number of iterations increases, it fills the area. With lines as thick as an Etch A Sketch, it seems to fill completely within 10 iterations or so.

A subtile point though is that, given any line thickness (except zero; in which case the lines wouldn’t exist!), it will eventually fill an area after some number of iterations. It’s another lesson in limits.

[Side note: This is a fun one to run on the robot and see it clear the whole screen!]

It too is defined rather simply, but recursively.

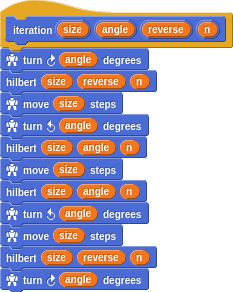
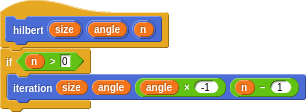
Sierpinski Triangle

The Sierpinski Triangle is something like the opposite to the Hilbert Curve. Rather than fill space, it’s area is reduced with each iteration until it disappears!

If we could draw with infinitesimally thin lines, then we could watch it reduce to nothing.

The program is similarly defined with a pair of mutually recursive sierpinski and iteration words.

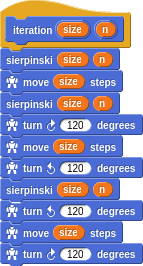
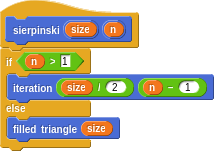
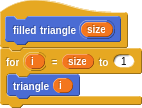
A filled triangle is just a bunch of triangles within triangles, by the way:

Dragon Curve

As a finale, here is a very beautiful one. Both the code and the result are quite interesting.

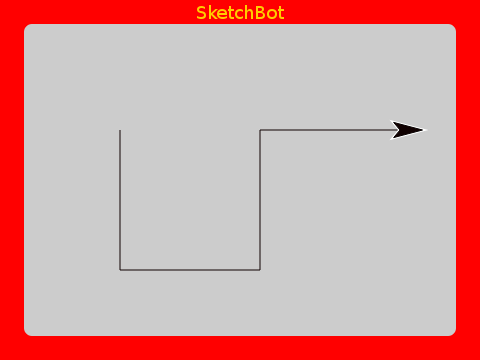
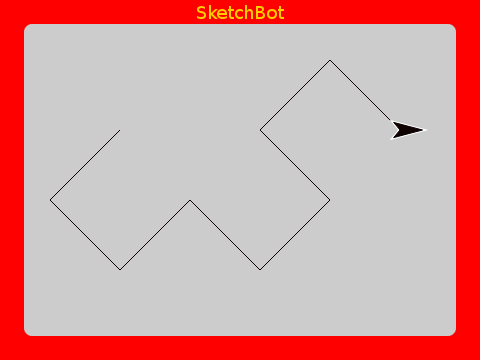
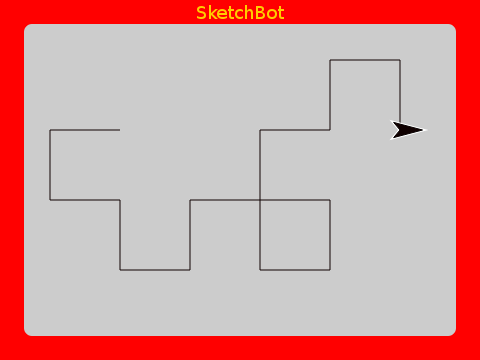
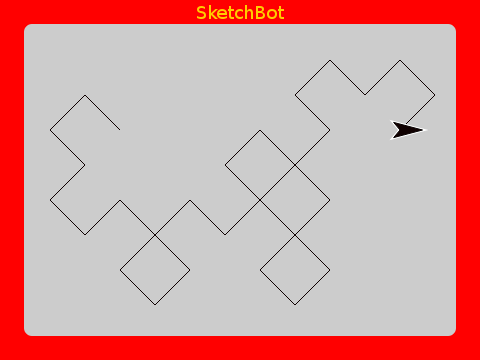
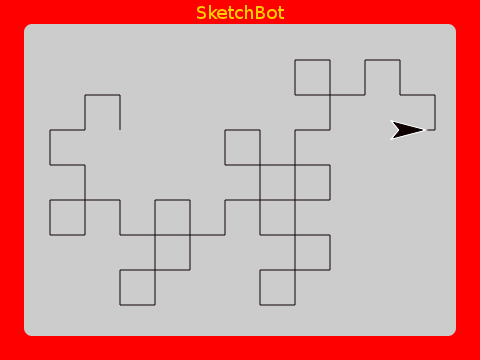
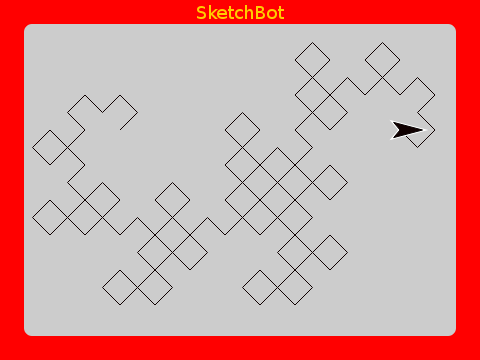
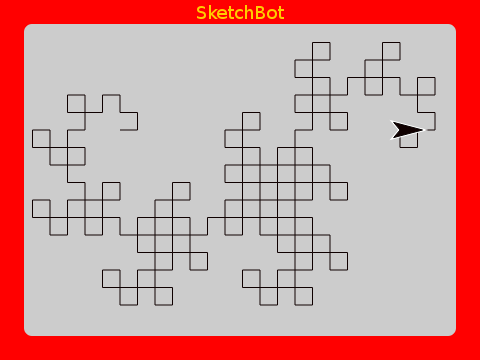
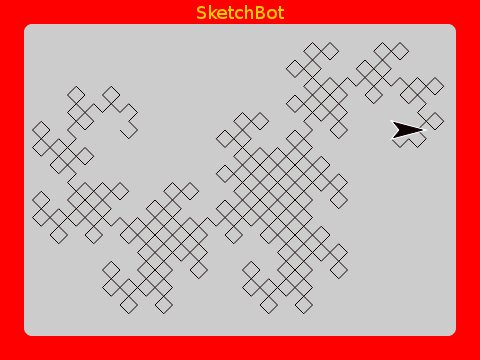
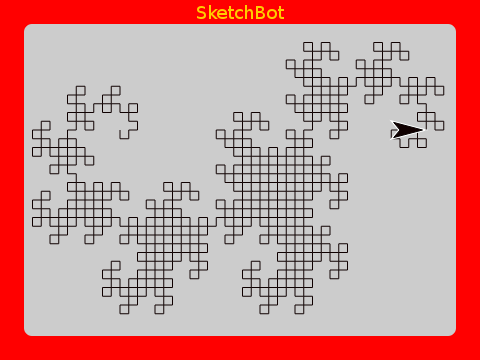
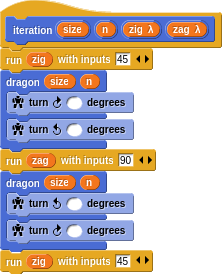
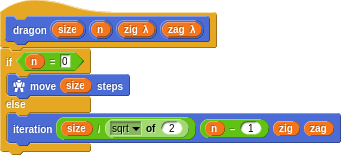
Using higher order functions makes the implementation very concise. It’s actually astounding the intricate beauty that can be defined with so little code.

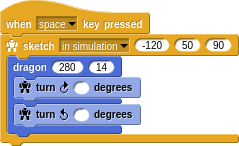
Have fun!